import torch
shuffled = torch.randperm(3 * 10**9)Torch vs Numpy shuffling
The purpose of this notebook is
to confirm Oskar’s analysis of problems with
torch.randperm.to show that it can be fixed by using numpy’s default random number generator or the PCG64DXSM generator specifically.
Oskar’s analysis implied that torch.randperm was not shuffling elements uniformly when the number of elements became very large, e.g., a billion or more (discord link). We confirmed this in the notebook below.
Specifically, this notebook confirms the following: If you start with 3 billion elements, tag them as belonging to ten “deciles” representing the first 10% of elements, the second 10% of elements, and so on, then shuffle all the elements, and then look at the first 10,000 elements, you do not find that the ten deciles are approximately uniformly distributed among the first 10,000 elements. Instead, torch.randperm is more likely to put the earlier elements (the lower deciles) into the first 10,000 elements of the shuffled collection. This corresponds to the bottom-left figure in Oskar’s original post.
We then found that switching to numpy’s random number generator, or to numpy’s PCG64DXSM generator, resolves this issue, and seems to produces an approximately uniform distribution of deciles within the first 10,000 elements of the shuffled collection..
We noticed that OLMo encountered a similar issue and resolved it by using a specific numpy generator (OLMo link ).
How uniform is torch’s shuffling with randperm?
Let’s generate an array representing a shuffling of the integers from 0 to (3 * 10^9 - 1)
shuffled_interval = shuffled[:10_000]shuffled_interval[:50]tensor([1994940797, 2347954103, 1691579500, 262720464, 2748298413, 2222743612,
1653995, 2342555504, 1440586107, 1077345365, 668539175, 2788525165,
117518658, 699722858, 1290958150, 2665873790, 2552246067, 2283160201,
177004620, 31564517, 2704208229, 1047164862, 25139448, 2216018010,
1004277474, 2440298876, 1240531966, 326584590, 943397255, 34365751,
150611451, 129402432, 2867900352, 1395077156, 256310869, 1292414480,
209935101, 440610241, 848544906, 407409817, 2578392564, 1809067203,
1297671095, 1108743574, 1086617589, 1632128034, 681494780, 1207082789,
1001392368, 879276196])[x.item() for x in shuffled_interval[:10]][1994940797,
2347954103,
1691579500,
262720464,
2748298413,
2222743612,
1653995,
2342555504,
1440586107,
1077345365]shuffled.shape[0]3000000000Define a decile function, which tells us which of the ten “decile” bins an element belonged to. That is, in the original unshuffled collection, was it in the first 10%, the second 10%, … and so on.
def decile(index, collection_size):
"Returns 1 to 10, for the decile of `index` within `collection_size`"
return 1 + int(index // (collection_size / 10))Verify the above function works as expected:
n = 20
[decile(x,n) for x in range(n)][1, 1, 2, 2, 3, 3, 4, 4, 5, 5, 6, 6, 7, 7, 8, 8, 9, 9, 10, 10]del nCompute the deciles for the first 10,000 shuffled values
deciles = [decile(x.item(),shuffled.shape[0]) for x in shuffled_interval]Let’s graph a histogram of the values in deciles.
%matplotlib inline
import matplotlib.pyplot as plt
plt.figure(figsize=(10, 6))
plt.hist(deciles, bins=range(1, 12), align='left', rwidth=0.8)
plt.xlabel('Decile')
plt.ylabel('Frequency')
plt.title('Histogram of Deciles, with torch.randperm')
plt.xticks(range(1, 11))
plt.show()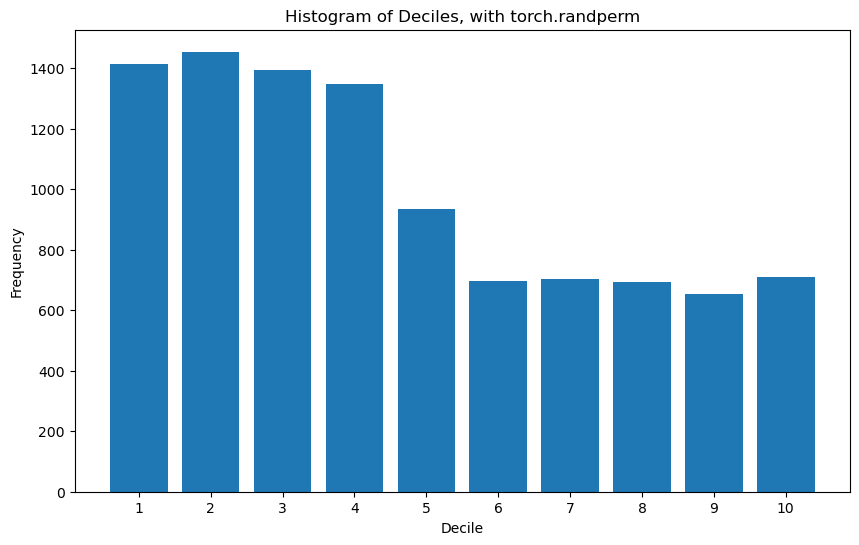
The above shows that torch’s shuffler is not producing a uniform shuffle over a collection of 3 B elements.
Now let’s try numpy with the PCG64DXSM generator.
Let’s generate an array representing a shuffling of the integers from 0 to (3 * 10^9 - 1), but using this random number generator from numpy: numpy.random.PCG64DXSM
import numpy as np
rng = np.random.Generator(np.random.PCG64DXSM())
shuffled = rng.permutation(3 * 10**9)
shuffled = torch.from_numpy(shuffled)
shuffled_interval = shuffled[:10_000]deciles = [decile(x.item(),shuffled.shape[0]) for x in shuffled_interval]%matplotlib inline
import matplotlib.pyplot as plt
plt.figure(figsize=(10, 6))
plt.hist(deciles, bins=range(1, 12), align='left', rwidth=0.8)
plt.xlabel('Decile')
plt.ylabel('Frequency')
plt.title('Histogram of Deciles with PCG64DXSM randomization')
plt.xticks(range(1, 11))
plt.show()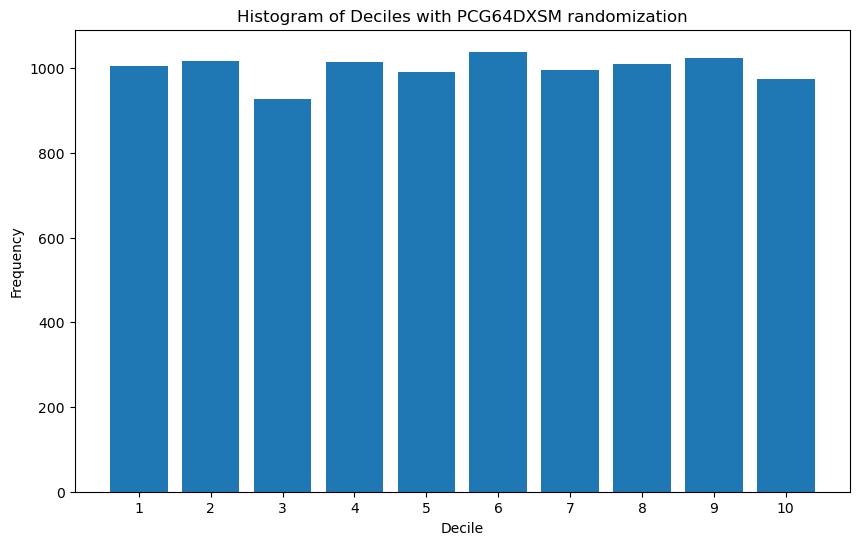
This is much closer to a uniform distribution.
Now let’s try with numpy’s default randperm.
import numpy as np
rng = np.random.default_rng()
shuffled = rng.permutation(3 * 10**9)
shuffled = torch.from_numpy(shuffled)
shuffled_interval = shuffled[:10_000]deciles = [decile(x.item(),shuffled.shape[0]) for x in shuffled_interval]%matplotlib inline
import matplotlib.pyplot as plt
plt.figure(figsize=(10, 6))
plt.hist(deciles, bins=range(1, 12), align='left', rwidth=0.8)
plt.xlabel('Decile')
plt.ylabel('Frequency')
plt.title('Histogram of Deciles with numpy default rng')
plt.xticks(range(1, 11))
plt.show()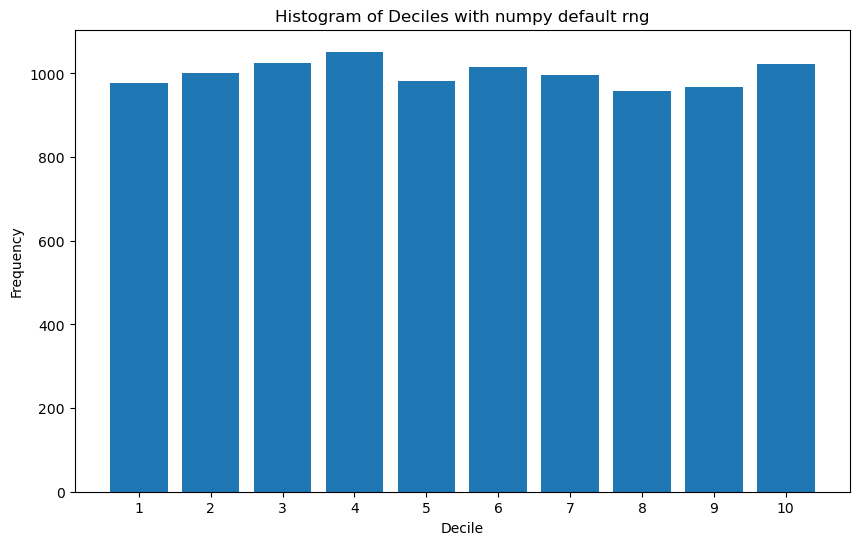
Version check
%%aip 0
Generate code to report my version of torchimport torch
print(f"PyTorch version: {torch.__version__}")PyTorch version: 2.4.0print(f"Numpy version: {np.__version__}")Numpy version: 2.0.1import os
cpu_count = os.cpu_count()
try:
with open("/proc/meminfo",'r') as mem:
meminfo = next(mem)
except:
meminfo ='unknown'
print(f"CPU: {cpu_count} logical cores")
print(meminfo)CPU: 16 logical cores
MemTotal: 131177156 kB