AI Prompt

I want to learn about markov random fields and what they can do in image analysis with your help. I have no formal education in math and I’m a self-taught python programmer and data scientist. I know what markov chains are.

AI Response

Thanks for letting me know your background! Since you’re familiar with Markov chains, that’s a great starting point. Before we dive into Markov Random Fields (MRFs), I’d like to check a few things to help customize our discussion:

1. How comfortable are you with probability concepts and graph theory?
2. What kinds of image analysis tasks are you particularly interested in? (e.g., segmentation, denoising, texture analysis)
3. Would you prefer to start with the intuitive concepts first, or would you like to see some practical examples right away?

Let me know your preferences, and we can begin exploring MRFs in a way that builds on your existing knowledge!

AI Prompt

I think I’m quite comfortable with probability concepts but I’m not very strong in graph theory, although I worked with a lot of graph problems in advent of code recently.

AI Response

Thanks for clarifying! Since you’re comfortable with probability but less familiar with graph theory, let me know if any graph concepts need more explanation as we go.

Before we continue, could you also tell me which image analysis tasks interest you most? This will help me provide relevant examples as we explore MRFs. For instance, they’re commonly used for: - Image denoising (cleaning up noisy images) - Image segmentation (separating objects/regions) - Texture synthesis - Image restoration

Which of these (or other applications) would you like to focus on?

AI Prompt

I came across markov random fields in image segmentation especially in post-processing after image segmentation with another algorithm in the context of aneurysm segmentation in MRI images. I learn best if I can get an intuitive understanding of the concept and what it is good for first and then we can dig into how it actually works after that.

AI Response

Ah, perfect! Medical image segmentation is a great context for understanding MRFs. Let me start with an intuitive explanation:

Imagine you’re looking at an MRI image where an algorithm has already tried to identify an aneurysm. For each pixel, the algorithm has made a decision: “aneurysm” or “not aneurysm”. But here’s the key insight that makes MRFs powerful: in real medical images, pixels don’t exist in isolation - they have a relationship with their neighboring pixels.

Think about it this way: if you see a single pixel labeled as “aneurysm”, but all its neighboring pixels are confidently labeled as “not aneurysm”, that single pixel is probably a mistake. This is where MRFs shine - they help clean up these inconsistencies by considering the context around each pixel.

Does this basic intuition make sense to you? If yes, we can move on to how MRFs formally represent these relationships between neighboring pixels.

AI Prompt

This intuition makes sense to me. It sounds a little bit like some kind of “smoothing”, but that makes sense when MRFs can also be used for image denoising

AI Response

Exactly! You’ve made a great connection there. The “smoothing” effect is indeed a common theme between denoising and post-segmentation cleanup.

Let me build on this intuition by explaining how MRFs formalize this idea. In an MRF, we create a graph where: 1. Each pixel is a node 2. Each node connects to its neighbors (usually the immediately adjacent pixels) 3. Each node has a probability distribution for its possible labels 4. The key part: the probability of a node’s label depends on both: - The original algorithm’s confidence in that label - The labels of its neighboring nodes

Would you like me to explain more about how these probabilities work, or would you prefer to see how this graph structure helps in practice first?

AI Prompt

show me how this graph structure helps in practice first (you can write python code if that helps your explanation, but only if it helps!)

AI Response

Let’s look at a simple practical example. Imagine we have a small 3x3 region of an image where our initial segmentation algorithm has labeled pixels as aneurysm (1) or not-aneurysm (0), with these initial labels:

import numpy as np

# Initial labels from our segmentation algorithm
initial_labels = np.array([
    [0, 0, 0],
    [0, 1, 0],  # Note the isolated '1' in the middle
    [0, 0, 0]
])

This is a classic case where we have a single “suspicious” pixel (the 1 in the middle) surrounded by different labels.

Would you like me to show you how MRF would consider this situation, or do you first have any questions about this setup?

import numpy as np

# Initial labels from our segmentation algorithm
initial_labels = np.array([
    [0, 0, 0],
    [0, 1, 0],  # Note the isolated '1' in the middle
    [0, 0, 0]
])

AI Prompt

no, the setup is clear to me.

AI Response

Great! Now, in an MRF, each pixel also has a confidence score from our original segmentation algorithm. Let’s add those (these numbers are made up for illustration):

# Confidence scores from original algorithm (higher = more confident)
confidence_scores = np.array([
    [0.8, 0.9, 0.8],  # Pretty confident these are not aneurysm (0)
    [0.7, 0.6, 0.8],  # Note middle pixel: only 0.6 confident it's aneurysm (1)
    [0.9, 0.8, 0.7]   # Pretty confident these are not aneurysm (0)
])

The MRF would look at: 1. The relatively low confidence (0.6) of our “suspicious” middle pixel 2. The fact that all neighboring pixels disagree with it 3. The high confidence of those neighboring pixels (0.7-0.9)

Based on this information, the MRF would likely decide this middle pixel was a mistake and should be relabeled as 0.

Would you like me to explain how the MRF mathematically makes this decision, or shall we look at a more complex example first?

AI Prompt

but do the confidence scores relate to how confident the algorithm is in it’s choice for the underlying label? so 0.6 for the middle pixel means its “0.6 sure” that a “1” is the correct label and the 0.8 for the upper left pixel means that it’s “0.8 sure” that the correct label is a “0”?

AI Response

Exactly right! You’ve understood it perfectly. The confidence score tells us “how sure” the algorithm is about its chosen label. So:

• For the middle pixel: 0.6 means “60% confident that this is a 1 (aneurysm)”
• For the upper left: 0.8 means “80% confident that this is a 0 (not aneurysm)”

This is crucial because it means the middle pixel’s classification wasn’t very confident to begin with (only 60%), while its neighbors are all quite confident (70-90%) that they’re not part of an aneurysm. This information helps the MRF decide how much weight to give to each pixel’s initial classification.

Would you like me to explain how the MRF uses these confidence scores mathematically, or do you have any other questions about the confidence scores first?

AI Prompt

it’s clear now. go on

AI Response

Great! Let’s look at how MRFs mathematically combine these two key pieces of information:

1. The “unary potential” - this represents the original confidence scores we just discussed
2. The “pairwise potential” - this represents how strongly we believe neighboring pixels should have the same label

The MRF tries to minimize an energy function that looks roughly like this:

# Pseudocode for energy at a single pixel
energy = unary_term + smoothness_weight * sum(pairwise_terms)

# where:
unary_term = -log(confidence_score)  # Higher confidence = lower energy
pairwise_term = penalty_if_different_from_neighbor

Would you like me to break down why we use these terms and what they mean, or would you prefer to see how this works in practice with our example?

AI Prompt

please explain to me what “energy” means in this context. I heard it also in the context of generative image modelling algorithms.

AI Response

In this context, “energy” is a way to measure how “good” or “bad” a particular solution is - the lower the energy, the better the solution. Think of it like a landscape where we’re trying to find the lowest valley:

1. When a configuration makes sense (like neighboring pixels having similar labels and respecting the original confidence scores), it has low energy.
2. When a configuration seems unlikely or problematic (like our isolated aneurysm pixel surrounded by non-aneurysm pixels), it has high energy.

The algorithm tries to find the configuration with the minimum total energy, which represents the most probable/sensible solution.

Is this general concept clear? If yes, I can explain why we specifically use -log(confidence_score) for the unary term.

AI Prompt

does it relate to entropy in any sense?

AI Response

Yes, excellent connection! The energy in MRFs is directly related to entropy and information theory. In fact, this relationship comes through the Boltzmann distribution from statistical physics, which connects probability and energy:

P(state) ∝ e^(-Energy/T)

Or, rearranging this: Energy ∝ -log(P(state))

This is exactly why we use -log(confidence_score) in our unary term! The confidence scores are probabilities, and we convert them to energies using this relationship.

Would you like me to explain more about this connection to entropy, or shall we continue with how the MRF uses these energy terms in practice?

AI Prompt

continue. what does the pairwise_term mean for example?

AI Response

The pairwise term represents the “cost” or penalty of having different labels between neighboring pixels. In its simplest form, it might look like this:

For any two neighboring pixels i and j: - If they have the same label: pairwise_term = 0 (no penalty) - If they have different labels: pairwise_term = 1 (or some other positive number)

However, in more sophisticated MRFs, this term might consider additional factors, like: - How different the actual pixel intensities are in the original image - Whether the pixels are separated by a strong edge - The physical distance between pixels

Would you like me to explain how these factors can be incorporated, or shall we look at how the unary and pairwise terms work together in our example?

AI Prompt

let’s go on with our example first. we’ll might come back later.

AI Response

Perfect! Let’s calculate the energy for our middle pixel in two scenarios. Remember our setup: - Current label is 1 (aneurysm) with 0.6 confidence - All 8 neighbors are 0 (non-aneurysm) with ~0.8 confidence

Let’s compare the energy if we: 1. Keep it as 1 (current state) 2. Change it to 0 (agreeing with neighbors)

Shall I walk through the energy calculation for the first scenario?

import math

energy = -math.log(0.6) + 8 * 1

energy

8.51082562376599

AI Prompt

this should be the energy for the first scenario, right?

AI Response

Yes, exactly! Let’s break down what this calculation means:

• -math.log(0.6) ≈ 0.51 is our unary term (from the original confidence)
• 8 * 1 = 8 is our total pairwise term (penalty of 1 for each of the 8 neighbors that disagree)
• Total energy ≈ 8.51

Should we calculate the energy for the second scenario (changing to 0) to compare? This would use the confidence that it’s NOT an aneurysm (1 - 0.6 = 0.4) for the unary term.

energy2 = -math.log(1-0.6) + 8* 0
energy2

0.916290731874155

AI Prompt

This should be the energy for scenario two. The energ is lower here, this means that the middle pixel should also be background and not an aneurysm, right?

AI Response

Exactly right! You’ve understood it perfectly. Since 0.916 < 8.51, the lower energy in scenario two tells us that labeling the middle pixel as background (0) is the more probable/sensible solution.

This makes intuitive sense because: 1. The original confidence wasn’t very high (only 0.6) 2. All neighbors agree it should be background 3. By changing to background, we eliminate all the pairwise penalties (8 * 0 = 0)

This is how MRFs can help “clean up” isolated pixels that don’t agree with their neighborhood context. Would you like to explore how this might work in a more complex scenario, or do you have questions about any part of what we’ve covered?

AI Prompt

No, that’s clear to me. And to properly post-process an image, you would do this calculation for every pixel correct?

AI Response

Yes, exactly! But there’s an important catch: when you update one pixel, it affects the energy calculations of its neighbors. So you can’t just do all pixels once in isolation.

There are different strategies to handle this: 1. Iterative approaches: repeatedly scan through all pixels until the changes stabilize 2. Message passing algorithms (like belief propagation) 3. Graph cut algorithms that can find the global minimum energy for certain types of energy functions

Would you like to learn more about any of these optimization approaches, or would you prefer to see how the pairwise terms can be made more sophisticated (like considering edge information) as we mentioned earlier?

AI Prompt

I don’t know whether it’s important for the understanding, but why does this “algorithm” is called markov random fields? so where does the name come from? I believe it has to do with the underlying theory, but I don’t know whether I need to know it, because the algorithm makes sense intuitively to me.

AI Response

The name comes from two key mathematical properties:

1. “Markov” - Just like in Markov chains, there’s a locality property: each pixel only directly depends on its neighbors, not on pixels far away. This is called the “Markov property.”

2. “Random Field” - It’s a field because we have variables (pixels) spread across a 2D space, and it’s random because we’re dealing with probabilities at each location.

The theory goes deeper into probability theory and statistical physics, but you’re right - you don’t need to understand all of that to use MRFs effectively. The intuitive understanding you have (local neighborhoods, energy minimization, confidence scores) is sufficient for most practical applications.

Would you like to know more about the theoretical background, or shall we move on to something else?

AI Prompt

No, let’s see how we can make the pairwise terms more sophisticated.

AI Response

Great! Instead of a simple binary penalty (0 or 1), we can make the pairwise term consider image features. Here are two common approaches:

1. Intensity-based weighting:

pairwise_term = exp(-|intensity1 - intensity2| / sigma)

This means: if two neighboring pixels have very different intensities (suggesting an edge), we reduce the penalty for them having different labels.

2. Edge-awareness:

pairwise_term = penalty * (1 - edge_strength)

Where edge_strength comes from an edge detector (like Sobel). This reduces the smoothing effect across strong edges.

Would you like me to show how either of these would change our earlier example, or would you prefer to learn about other ways to make the pairwise term more sophisticated?

AI Prompt

The intensity-based weighting sounds very intuitive and would probably work quite well for MRI images, where we want to segment part of vessels which have another intensity as the surounding tissue.

AI Response

Exactly! You’ve made a perfect connection to the medical imaging context. In MRI images, aneurysms and vessels often appear with different intensities compared to surrounding tissue.

Let’s consider how this would work: 1. In areas where vessel/aneurysm meets normal tissue, there’s a natural intensity difference 2. The exp(-|intensity1 - intensity2| / sigma) term would be small at these boundaries 3. This allows the segmentation boundary to follow the actual vessel edges, rather than being over-smoothed

The parameter sigma controls how sensitive we are to intensity differences: - Small sigma: very sensitive to intensity changes - Large sigma: more tolerant of gradual intensity variations

Would you like to see how different sigma values would affect the pairwise term, or shall we discuss how to choose an appropriate sigma for MRI images?

AI Prompt

No. let’s actually implement it using a toy example again.

AI Response

Sure! Let’s create a simple example with a small image patch that mimics a vessel-like intensity pattern. We’ll calculate the energy with intensity-weighted pairwise terms:

import numpy as np

# Create a 3x3 image patch with intensities
# Higher values represent brighter pixels (like a vessel in MRI)
intensities = np.array([
    [50, 50, 50],
    [50, 200, 50],  # Middle pixel is bright like a vessel
    [50, 50, 50]
])

# Initial segmentation confidence (like before)
confidence_scores = np.array([
    [0.8, 0.8, 0.8],  # Confident these are background
    [0.7, 0.6, 0.8],  # Middle pixel: 0.6 confident it's vessel
    [0.8, 0.8, 0.8]
])

Would you like me to show how to calculate the energy with intensity-weighted pairwise terms for this example?

AI Prompt

Maybe use a more appropriate confidence score representation. Since image segmentation is basically binary classification on a pixel-level, it’s more appropriate to model it with scores from 0 to 1 where a number < 0.5 would lead to a classification as background and a number > 0.5 as foreground (the threshold can obviously be moved, but let’s keep it that way).

AI Response

Ah yes, that’s a much better way to represent it! Let’s revise our example with this more appropriate confidence scoring:

# Same intensity pattern
intensities = np.array([
    [50, 50, 50],
    [50, 200, 50],  # Middle pixel is bright like a vessel
    [50, 50, 50]
])

# Confidence scores where:
# > 0.5 means "confident it's vessel"
# < 0.5 means "confident it's background"
# 0.5 would be "completely uncertain"
confidence_scores = np.array([
    [0.2, 0.2, 0.2],  # Pretty confident these are background
    [0.3, 0.7, 0.2],  # Middle pixel: somewhat confident it's vessel
    [0.2, 0.2, 0.2]
])

Now 0.7 for the middle pixel means it’s somewhat confident it’s a vessel, while 0.2 for the surroundings means they’re quite confident to be background. Shall we calculate the energy using these more intuitive scores?

# Same intensity pattern
intensities = np.array([
    [50, 50, 50],
    [50, 200, 50],  # Middle pixel is bright like a vessel
    [50, 50, 50]
])

# Confidence scores where:
# > 0.5 means "confident it's vessel"
# < 0.5 means "confident it's background"
# 0.5 would be "completely uncertain"
confidence_scores = np.array([
    [0.2, 0.2, 0.2],  # Pretty confident these are background
    [0.3, 0.7, 0.2],  # Middle pixel: somewhat confident it's vessel
    [0.2, 0.2, 0.2]
])

AI Prompt

Yes, let’s go on with the energy calculation.

AI Response

Great! Let’s calculate the energy for the middle pixel in both scenarios, but this time with intensity-weighted pairwise terms. We’ll use sigma = 50 for this example:

import math

def pairwise_weight(intensity1, intensity2, sigma=50):
    return math.exp(-abs(intensity1 - intensity2) / sigma)

# Get middle pixel's intensity and its neighbors' intensities
middle_intensity = intensities[1,1]  # 200
neighbor_intensities = [
    intensities[0,1], intensities[2,1],  # top, bottom
    intensities[1,0], intensities[1,2],  # left, right
    intensities[0,0], intensities[0,2],  # top corners
    intensities[2,0], intensities[2,2]   # bottom corners
]

# Calculate weights based on intensity differences
weights = [pairwise_weight(middle_intensity, n, sigma=50) for n in neighbor_intensities]

# Let's see what these weights look like first
print("Pairwise weights for each neighbor:", weights)

Would you like to see these weights before we continue with the full energy calculation?

import math

def pairwise_weight(intensity1, intensity2, sigma=50):
    return math.exp(-abs(intensity1 - intensity2) / sigma)

middle_intensity = intensities[1,1]
middle_intensity

200

neighbor_intensities = [
    intensities[0,1], intensities[2,1],  # top, bottom
    intensities[1,0], intensities[1,2],  # left, right
    intensities[0,0], intensities[0,2],  # top corners
    intensities[2,0], intensities[2,2]   # bottom corners
]

weights = [pairwise_weight(middle_intensity, n, sigma=50) for n in neighbor_intensities]
weights

[0.049787068367863944,
 0.049787068367863944,
 0.049787068367863944,
 0.049787068367863944,
 0.049787068367863944,
 0.049787068367863944,
 0.049787068367863944,
 0.049787068367863944]

AI Prompt

Let’s go on.

AI Response

Now let’s calculate the total energy for both scenarios, using these weights. For each scenario, we’ll combine: 1. The unary term (from confidence scores) 2. The weighted pairwise terms

# Scenario 1: Middle pixel labeled as vessel (1)
unary1 = -math.log(0.7)  # Using confidence score for vessel
pairwise1 = sum(w * 1 for w in weights)  # All neighbors are different (0)

energy1 = unary1 + pairwise1
print(f"Energy when labeled as vessel: {energy1}")

# Scenario 2: Middle pixel labeled as background (0)
unary2 = -math.log(0.3)  # Using 1 - 0.7 for background confidence
pairwise2 = sum(w * 0 for w in weights)  # All neighbors are same (0)

energy2 = unary2 + pairwise2
print(f"Energy when labeled as background: {energy2}")

Would you like me to explain what these results tell us about which label the MRF prefers?

energy1 = -math.log(0.7) + sum(w * 1 for w in weights)
energy1

0.7549714908816441

energy2 = -math.log(0.3) + sum(w * 0 for w in weights)
energy2

1.2039728043259361

AI Prompt

So in this case, the energy is lower when we classify the middle pixel as foreground (as we did). Does it make sense to not only incorporate the intensites of the neighboring pixels in our pairwise term but also their confidence scores?

AI Response

Yes, absolutely! That’s a great insight. By incorporating both intensity differences and confidence scores in the pairwise term, we can make even more informed decisions. The intuition would be:

• If a neighbor has high confidence (far from 0.5) in its label, its influence should be stronger
• If a neighbor has low confidence (close to 0.5), maybe we shouldn’t weight its opinion as heavily

We could modify our pairwise weight function to something like:

def pairwise_weight(intensity1, intensity2, conf1, conf2, sigma=50):
    intensity_weight = math.exp(-abs(intensity1 - intensity2) / sigma)
    confidence_weight = abs(conf1 - 0.5) * abs(conf2 - 0.5)  # High when both confident
    return intensity_weight * confidence_weight

Would you like to see how this changes our energy calculations?

def pairwise_weight(intensity1, intensity2, conf1, conf2, sigma=50):
    intensity_weight = math.exp(-abs(intensity1 - intensity2) / sigma)
    confidence_weight = abs(conf1 - 0.5) * abs(conf2 - 0.5)  # High when both confident
    return intensity_weight * confidence_weight

AI Prompt

yes, show me how the energy calculation would differ here.

AI Response

Let’s calculate the new weights and energies with both intensity and confidence information:

# Get middle pixel's values and neighbors
middle_intensity = intensities[1,1]  # 200
middle_conf = confidence_scores[1,1]  # 0.7

neighbor_intensities = [
    intensities[0,1], intensities[2,1],  # top, bottom
    intensities[1,0], intensities[1,2],  # left, right
    intensities[0,0], intensities[0,2],  # top corners
    intensities[2,0], intensities[2,2]   # bottom corners
]

neighbor_confidences = [
    confidence_scores[0,1], confidence_scores[2,1],
    confidence_scores[1,0], confidence_scores[1,2],
    confidence_scores[0,0], confidence_scores[0,2],
    confidence_scores[2,0], confidence_scores[2,2]
]

# Calculate new weights considering both intensity and confidence
new_weights = [pairwise_weight(middle_intensity, n_int, middle_conf, n_conf) 
               for n_int, n_conf in zip(neighbor_intensities, neighbor_confidences)]

print("New weights (with confidence):", new_weights)

# Calculate energies with new weights
energy1_new = -math.log(0.7) + sum(w * 1 for w in new_weights)
energy2_new = -math.log(0.3) + sum(w * 0 for w in new_weights)

print(f"\nNew energy when labeled as vessel: {energy1_new}")
print(f"New energy when labeled as background: {energy2_new}")

Let’s compare these results with our previous ones and see how incorporating confidence changes things!

# Get middle pixel's values and neighbors
middle_intensity = intensities[1,1]  # 200
middle_conf = confidence_scores[1,1]  # 0.7

neighbor_intensities = [
    intensities[0,1], intensities[2,1],  # top, bottom
    intensities[1,0], intensities[1,2],  # left, right
    intensities[0,0], intensities[0,2],  # top corners
    intensities[2,0], intensities[2,2]   # bottom corners
]

neighbor_confidences = [
    confidence_scores[0,1], confidence_scores[2,1],
    confidence_scores[1,0], confidence_scores[1,2],
    confidence_scores[0,0], confidence_scores[0,2],
    confidence_scores[2,0], confidence_scores[2,2]
]

# Calculate new weights considering both intensity and confidence
new_weights = [pairwise_weight(middle_intensity, n_int, middle_conf, n_conf) 
               for n_int, n_conf in zip(neighbor_intensities, neighbor_confidences)]

print("New weights (with confidence):", new_weights)

# Calculate energies with new weights
energy1_new = -math.log(0.7) + sum(w * 1 for w in new_weights)
energy2_new = -math.log(0.3) + sum(w * 0 for w in new_weights)

print(f"\nNew energy when labeled as vessel: {energy1_new}")
print(f"New energy when labeled as background: {energy2_new}")

New weights (with confidence): [0.002987224102071836, 0.002987224102071836, 0.0019914827347145576, 0.002987224102071836, 0.002987224102071836, 0.002987224102071836, 0.002987224102071836, 0.002987224102071836]

New energy when labeled as vessel: 0.37957699538794987
New energy when labeled as background: 1.2039728043259361

AI Prompt

This makes perfect sense to me. great.

AI Response

I’m glad it makes sense! You’ve now seen how MRFs can combine multiple sources of information: 1. Original confidence scores (unary term) 2. Intensity differences between pixels 3. Confidence levels of neighboring pixels

This makes them very powerful for post-processing segmentation results, especially in medical imaging where you have both intensity information and initial segmentation confidences to work with.

Would you like to explore any other aspects of MRFs, such as: - How to handle different neighborhood sizes - Other types of pairwise terms - The optimization algorithms we mentioned earlier - Or something else?

AI Prompt

Yes, I’m really interested in how to optimize a whole image with that and not only a single pixel. Since everything is interconnected, this seems to be non-trivial.

AI Response

Yes, exactly! Optimizing the whole image is challenging because changing one pixel affects its neighbors, which affects their neighbors, and so on. Let me explain the main approaches:

1. Iterative Optimization (simplest):
   • Scan through all pixels repeatedly
   • Update each pixel based on current neighbor states
   • Continue until changes are minimal or a max iteration count is reached
   • However, this might get stuck in local minima
2. Graph Cuts (more sophisticated):
   • Treats the problem as finding a minimum cut in a graph
   • Can find the global optimum for certain types of energy functions
   • Very efficient for binary labeling problems (like our vessel/background case)

Would you like me to explain one of these approaches in more detail? The graph cuts method is particularly interesting for binary segmentation like your use case.

AI Prompt

I’m not really firm in graph theory, so I think the iterative optimization technique might be more intuitive for me.

AI Response

Let’s walk through the iterative optimization approach with a simple example. The basic algorithm would be:

1. Start with initial labels from our confidence scores (threshold at 0.5)
2. For each iteration:
   • Visit each pixel
   • Calculate energy for both possible labels (like we did before)
   • Choose the label with lower energy
   • Keep track of how many pixels changed
3. Stop when very few pixels change (or after max iterations)

Would you like me to show you how this would work with a slightly larger example image (say 5x5) to see how the iterations progress? We can visualize how the segmentation changes with each pass.

AI Prompt

Yes, please show me.

AI Response

Let’s create a 5x5 example with a simple vessel-like pattern. First, let’s set up our test data:

import numpy as np
import matplotlib.pyplot as plt

# Create a 5x5 image with a diagonal vessel-like pattern
intensities = np.ones((5, 5)) * 50  # background
vessel_path = [(0,0), (1,1), (2,2), (3,3), (4,4)]  # diagonal vessel
for i, j in vessel_path:
    intensities[i,j] = 200  # vessel is brighter

# Initial confidence scores (simulating output from a segmentation algorithm)
confidence_scores = np.ones((5, 5)) * 0.2  # background confidence
for i, j in vessel_path:
    confidence_scores[i,j] = 0.7  # vessel confidence
    
# Add some noise to make it interesting
confidence_scores += np.random.normal(0, 0.1, (5,5))
confidence_scores = np.clip(confidence_scores, 0.1, 0.9)  # keep in reasonable range

# Visualize initial state
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(10,5))
ax1.imshow(intensities, cmap='gray')
ax1.set_title('Intensities')
ax2.imshow(confidence_scores, cmap='RdBu')
ax2.set_title('Initial Confidence Scores')
plt.show()

Would you like me to show how to implement one iteration of the optimization before we run the full algorithm?

import numpy as np
import matplotlib.pyplot as plt

# Create a 5x5 image with a diagonal vessel-like pattern
intensities = np.ones((5, 5)) * 50  # background
vessel_path = [(0,0), (1,1), (2,2), (3,3), (4,4)]  # diagonal vessel
for i, j in vessel_path:
    intensities[i,j] = 200  # vessel is brighter

# Initial confidence scores (simulating output from a segmentation algorithm)
confidence_scores = np.ones((5, 5)) * 0.2  # background confidence
for i, j in vessel_path:
    confidence_scores[i,j] = 0.7  # vessel confidence
    
# Add some noise to make it interesting
confidence_scores += np.random.normal(0, 0.1, (5,5))
confidence_scores = np.clip(confidence_scores, 0.1, 0.9)  # keep in reasonable range

# Visualize initial state
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(10,5))
ax1.imshow(intensities, cmap='gray')
ax1.set_title('Intensities')
ax2.imshow(confidence_scores, cmap='RdBu')
ax2.set_title('Initial Confidence Scores')
plt.show()

import matplotlib.pyplot as plt

intensities = np.ones((5, 5)) * 50

vessel_path = [(0,0), (1,1), (2,2), (3,3), (4,4)]  # diagonal vessel
for i, j in vessel_path:
    intensities[i,j] = 200

confidence_scores = np.ones((5, 5)) * 0.2  # background confidence
for i, j in vessel_path:
    confidence_scores[i,j] = 0.7

confidence_scores += np.random.normal(0, 0.1, (5,5))
confidence_scores = np.clip(confidence_scores, 0.1, 0.9)

confidence_scores

array([[0.7363559 , 0.19017259, 0.27827538, 0.26580663, 0.17610686],
       [0.17123352, 0.49072809, 0.17748012, 0.20551782, 0.2261018 ],
       [0.17191357, 0.21427002, 0.72786857, 0.1       , 0.30914427],
       [0.2611385 , 0.29225269, 0.2453294 , 0.81035347, 0.28130468],
       [0.14035129, 0.1887681 , 0.39568265, 0.35623788, 0.74101395]])

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(10,5))
ax1.imshow(intensities, cmap='gray')
ax1.set_title('Intensities')
ax2.imshow(confidence_scores, cmap='RdBu')
ax2.set_title('Initial Confidence Scores')
plt.show()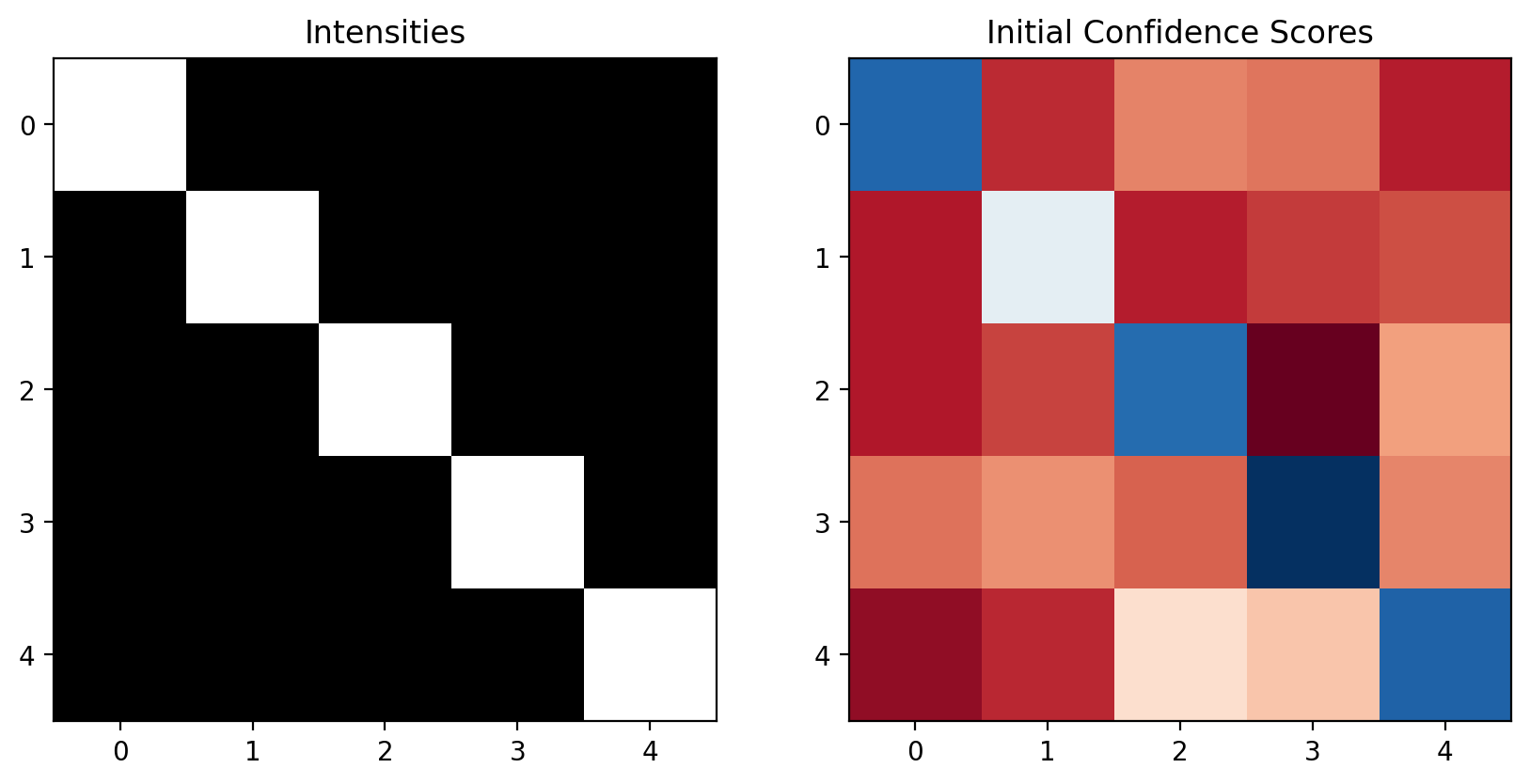

AI Prompt

Okay, I’m all set. Now we need to loop over each pixel and do our spiel. Let’s use the weight function with the intensities and confidence scores. write very concise code please.

AI Response

Here’s a concise implementation of one iteration of the optimization:

def optimize_one_iteration(intensities, confidence_scores, current_labels, sigma=50):
    height, width = intensities.shape
    changes = 0
    
    for i in range(height):
        for j in range(width):
            # Get neighbors within bounds
            neighbors = [(i+di, j+dj) for di, dj in [(-1,0), (1,0), (0,-1), (0,1)]
                       if 0 <= i+di < height and 0 <= j+dj < width]
            
            # Calculate energy for both labels
            energies = []
            for label in [0, 1]:
                conf = confidence_scores[i,j] if label == 1 else (1 - confidence_scores[i,j])
                unary = -np.log(conf)
                pairwise = sum(pairwise_weight(intensities[i,j], intensities[ni,nj], 
                                             confidence_scores[i,j], confidence_scores[ni,nj]) 
                              for ni, nj in neighbors)
                energies.append(unary + pairwise)
            
            # Update if better label found
            new_label = np.argmin(energies)
            if new_label != current_labels[i,j]:
                current_labels[i,j] = new_label
                changes += 1
                
    return changes

# Initialize labels
current_labels = (confidence_scores > 0.5).astype(int)

Would you like to run this for several iterations and see how the segmentation evolves?

def optimize_one_iteration(intensities, confidence_scores, current_labels, sigma=50):
    height, width = intensities.shape
    changes = 0
    
    for i in range(height):
        for j in range(width):
            # Get neighbors within bounds
            neighbors = [(i+di, j+dj) for di, dj in [(-1,0), (1,0), (0,-1), (0,1)]
                       if 0 <= i+di < height and 0 <= j+dj < width]
            
            # Calculate energy for both labels
            energies = []
            for label in [0, 1]:
                conf = confidence_scores[i,j] if label == 1 else (1 - confidence_scores[i,j])
                unary = -np.log(conf)
                pairwise = sum(pairwise_weight(intensities[i,j], intensities[ni,nj], 
                                             confidence_scores[i,j], confidence_scores[ni,nj]) 
                              for ni, nj in neighbors)
                energies.append(unary + pairwise)
            
            # Update if better label found
            new_label = np.argmin(energies)
            if new_label != current_labels[i,j]:
                current_labels[i,j] = new_label
                changes += 1
                
    return changes

# Initialize labels
current_labels = (confidence_scores > 0.5).astype(int)

AI Prompt

now write the code for me please. let it run for 5 iterations and save each iteration so that we can visualize how they change.

AI Response

# Store labels for each iteration
all_labels = [current_labels.copy()]

# Run 5 iterations
for iteration in range(5):
    changes = optimize_one_iteration(intensities, confidence_scores, current_labels)
    all_labels.append(current_labels.copy())
    print(f"Iteration {iteration+1}: {changes} pixels changed")

# Visualize evolution
fig, axes = plt.subplots(2, 3, figsize=(15, 10))
axes = axes.ravel()

axes[0].imshow(intensities, cmap='gray')
axes[0].set_title('Original Intensities')

for i in range(5):
    axes[i+1].imshow(all_labels[i], cmap='binary')
    axes[i+1].set_title(f'Iteration {i}')

plt.tight_layout()
plt.show()

This will show us how the segmentation evolves over the iterations. Would you like me to explain what we’re seeing in the results?

# Store labels for each iteration
all_labels = [current_labels.copy()]

# Run 5 iterations
for iteration in range(12):
    changes = optimize_one_iteration(intensities, confidence_scores, current_labels)
    all_labels.append(current_labels.copy())
    print(f"Iteration {iteration+1}: {changes} pixels changed")

# Visualize evolution
fig, axes = plt.subplots(4, 3, figsize=(15, 10))
axes = axes.ravel()

axes[0].imshow(intensities, cmap='gray')
axes[0].set_title('Original Intensities')

for i in range(11):
    axes[i+1].imshow(all_labels[i], cmap='binary')
    axes[i+1].set_title(f'Iteration {i}')

plt.tight_layout()
plt.show()

Iteration 1: 0 pixels changed
Iteration 2: 0 pixels changed
Iteration 3: 0 pixels changed
Iteration 4: 0 pixels changed
Iteration 5: 0 pixels changed
Iteration 6: 0 pixels changed
Iteration 7: 0 pixels changed
Iteration 8: 0 pixels changed
Iteration 9: 0 pixels changed
Iteration 10: 0 pixels changed
Iteration 11: 0 pixels changed
Iteration 12: 0 pixels changed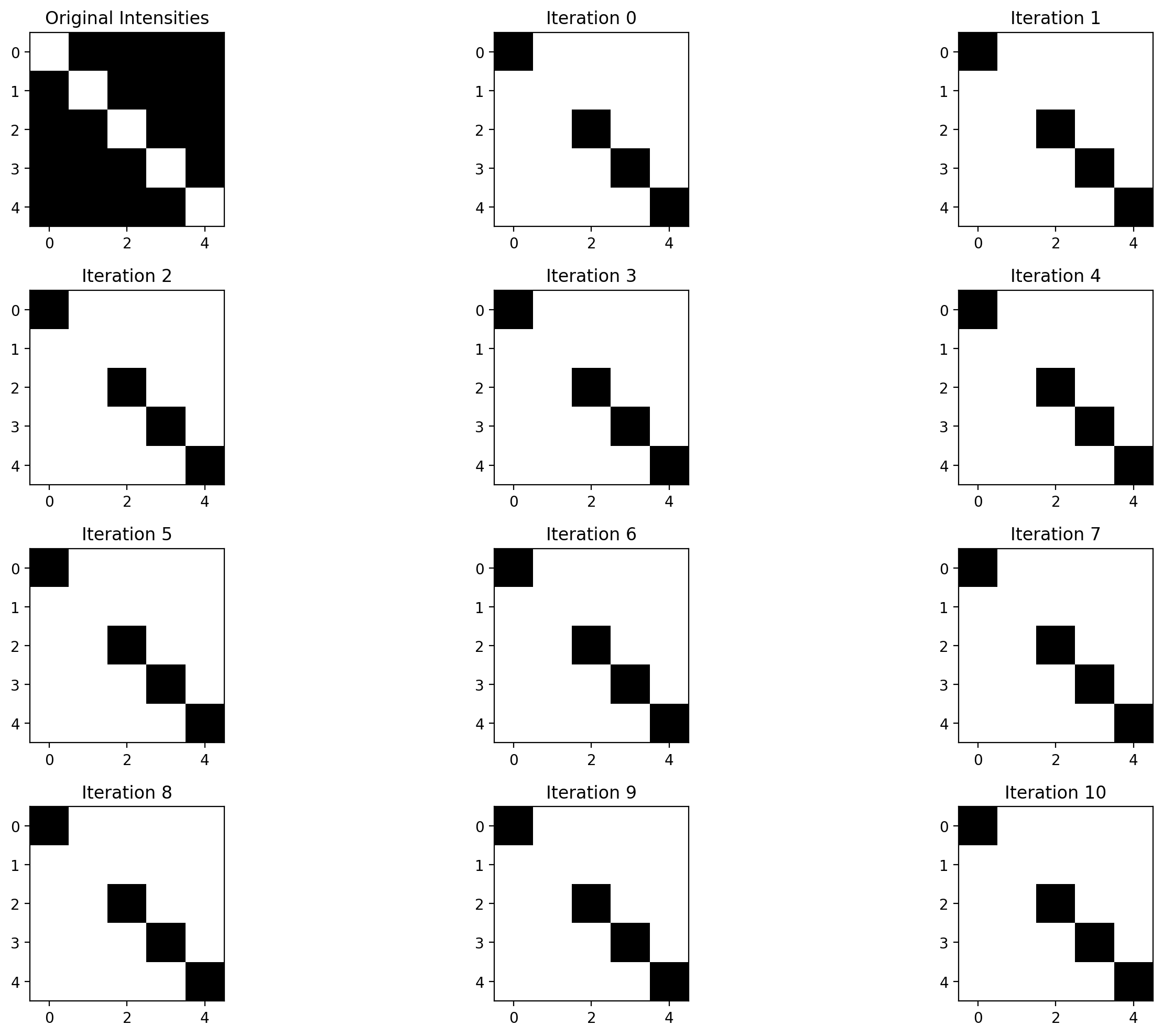

AI Prompt

well this works, somewhat I guess :D

AI Response

Ah yes, we got 0 changes in each iteration, which means our initial segmentation (based on confidence scores > 0.5) was already at a local minimum! This can happen with our energy function.

We could try a few things to make it more interesting: 1. Adjust the sigma parameter to change how much we care about intensity differences 2. Add more noise to our confidence scores 3. Change the weighting between unary and pairwise terms

Would you like to try any of these modifications to see more evolution in the segmentation?

Also, notice that our initial segmentation actually did a decent job following the diagonal vessel pattern, which is why it didn’t change much. This suggests our confidence scores were already pretty good!