Complex number representations

Complex numbers are numbers with two components: a real part \(x\) and an imaginary part \(y\). We can visually represent this as a point on a 2D plane.

Normalized States

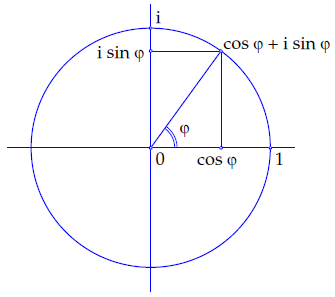
In quantum computing we generally only encounter vectors where \(r=1\), since quantum states must be normalized. This means that we can simplify our equations to:

\[z = e^{i\theta} = cos(\theta) + i sin(\theta)\]

A benefit of normalized complex numbers is that they can be visualized on a unit circle, like so:

An example of a normalized state you will encounter in quantum computing is the superposition of two states:

\[z = \frac{1}{\sqrt{2}} + \frac{1}{\sqrt{2}}i\]

This is the case because \(\sqrt{a^2 + b^2} = 1\) with \(z = a + bi\):

\[|z| = \sqrt{\left(\frac{1}{\sqrt{2}}\right)^2 + \left(\frac{1}{\sqrt{2}}\right)^2} = \sqrt{\frac{1}{2} + \frac{1}{2}} = \sqrt{1} = 1\]

z = (1 / np.sqrt(2)) + (1 / np.sqrt(2)) * 1j
z

(0.7071067811865475+0.7071067811865475j)

theta = np.angle(z)
theta

0.7853981633974483

First we check that \(z = cos(\theta) + i sin(\theta)\) for a normalized state:

norm_polar_form = np.cos(theta) + np.sin(theta) * 1j
norm_polar_form

(0.7071067811865476+0.7071067811865475j)

np.allclose(z, norm_polar_form)

True

Now we check that \(z = e^{i\theta}\) for a normalized state:

norm_exp_form = np.exp(1j * theta)
norm_exp_form

(0.7071067811865476+0.7071067811865475j)

np.allclose(z, norm_exp_form)

True

Complex Conjugate (\(*\))

An operation we often encounter in quantum computing is the complex conjugate (\(*\)). This simply means that the complex part of the number is flipped. With NumPy we can use the np.conj function to get the complex conjugate.

\[z = a + bi\]

\[z^* = a - bi\]

z = 3 + 2j
z

(3+2j)

# 3+2j -> 3-2j
np.conj(z)

(3-2j)

For NumPy numbers and arrays we can call .conj() directly on the object.

# 3+2j -> 3-2j
np.complex128(z).conj()

(3-2j)

# [1+2j, 3+4j] -> [1-2j, 3-4j]
np.array([1 + 2j, 3 + 4j]).conj()

array([1.-2.j, 3.-4.j])

Conjugate Transpose (\(\dagger\))

Another common quantum computing operation you will encounter is the conjugate transpose (\(\dagger\)). This is simply an extension of the complex conjugate where we take both the complex conjugate (\(*\)) and the transpose \(^T\). The conjugate transpose is formally denoted by a dagger (\(\dagger\)) and is sometimes called the “Dagger operation”. In quantum mechanics you may also encounter the terms “Hermitian conjugate” or “Hermitian adjoint” for this operation. In NumPy we simply add .T to our complex conjugate (.conj().T) to get the conjugate transpose.

For vectors the conjugate transpose simplify flips a row vector into a column vector and vice versa. It also flips the sign of the imaginary part (\(*\)): \[v = \begin{bmatrix} a_1 & a_2 & \cdots & a_n \end{bmatrix}\]

\[v^\dagger = \begin{bmatrix} a_1^* \\ a_2^* \\ \vdots \\ a_n^* \end{bmatrix}\]

For matrices the conjugate transpose flips the rows and columns and again flips the sign of the imaginary part (\(*\)):

\[A = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{bmatrix}\]

\[A^\dagger = \begin{bmatrix} a_{11}^* & a_{21}^* & \cdots & a_{n1}^* \\ a_{12}^* & a_{22}^* & \cdots & a_{n2}^* \\ \vdots & \vdots & \ddots & \vdots \\ a_{1n}^* & a_{2n}^* & \cdots & a_{nn}^* \end{bmatrix}\]

vector = np.array([[1 + 2j, 3 + 4j]])
vector

array([[1.+2.j, 3.+4.j]])

# [[1+2j, 3+4j]] -> [[1-2j,
#                    [3-4j]]
vector.conj().T

array([[1.-2.j],
       [3.-4.j]])

matrix = np.array([[1 + 2j, 3 + 4j], [5 + 6j, 7 + 8j]])
matrix

array([[1.+2.j, 3.+4.j],
       [5.+6.j, 7.+8.j]])

# [[1+2j, 3+4j] -> [[1-2j, 5-6j]
#  [5+6j, 7+8j]]    [3-4j, 7-8j]]
matrix.conj().T

array([[1.-2.j, 5.-6.j],
       [3.-4.j, 7.-8.j]])

That is the core of what you should know about complex numbers to get started with quantum computing! For additional video instruction I would recommend the following videos: - Quantum Computing Course: 0.1 Introduction to Imaginary and Complex Numbers - Quantum Computing Course: 0.2 Complex Numbers on the Number Plane - Imaginary numbers aren’t imaginary - Complex numbers aren’t complex - The Square Root of Negative One - Complex Numbers in Quantum Mechanics

Continue with the q4p course: - On Github - On Kaggle

If you are viewing this notebook on Kaggle, consider giving an upvote and leaving a comment. Your feedback is very welcome and I will try to implement your suggestions in this notebook.

If you are viewing this notebook on Github, please consider giving a star to the repository.

This notebook is part of the q4p (Quantum Computing for Programmers) series. The original notebook can be found on Github.